1º ANO/LAB. MATEMÁTICA

                                                                           ROTEIRO DE ESTUDO

Componente Curricular: Matemática
Tema Norteador: CONSUMISMO

Laboratório: Laboratório de Aprendizagem de Matemática

Carga horária: 5H semanais
A atividade é referente: 22/06 à 06/07/2020

Caro estudante,

Este Roteiro tem como objetivo orientar os seus estudos individuais, durante esse período de atividades não presenciais. procure cumprir com responsabilidade e empenho as atividades propostas, anote suas dúvidas para tirá-las com o professor, nos momentos programados. Faça todas as anotações no seu caderno e diário de bordo.

CONSUMISMO

Consumo Emocional O mercado concentra-se nos anseios, os quais são gerados a partir da disseminação do que é bom ou ruim para o indivíduo. As marcas, por sua vez, aproveitam-se desse estado emocional de incertezas e lançam, constantemente, seus produtos a fim de dar o devido conforto material, de que determinado produto atende ou não ao que sendo posto como “indicado” ou “não indicado”. O frenesi consumidor, mutilação da vida: no rastro traçado pela crítica marxista da religião, filósofos e sociólogos não deixaram de interpretar a propensão a comprar, como um novo ópio do povo, destinado a compensar o tédio do trabalho fragmentado, as falhas da mobilidade social, a infelicidade da solidão. ‘sofro, logo compro’: quanto mais o indivíduo está isolado ou frustrado, mais busca consolos nas felicidades imediatas da mercadoria (LIPOVETSKY, 2007, p. 60).

Nesse sentido, o “hiperconsumo” dá sustentação a um estado de espírito que vislumbra a atitude e a identidade construída a partir da individualização dos desejos e da busca incansável pelo prazer imediato. O Prazer ocupa o centro da vida.

A sociedade investe em mecanismos de viver com prazer. O mercado, por sua vez, cria várias opções de lazer de modo a satisfazer essa tendência. O efêmero, as inovações nos produtos geram as novidades que se tornam o atrativo. O consumidor é seduzido pela inovação constante, o que ocasiona emoção sem racionalidade. Esse comportamento segue causando dependência e descontrole financeiro em muitas famílias.

Em alguns casos, quanto mais o indivíduo está isolado ou frustrado, mais este busca por consolos nas alegrias imediatas do ato de comprar. Há, portanto, uma constante renovação dos produtos e mudança nos modelos e estilos de modas. “Sofro, logo compro.”

Se, por um lado, temos um consumidor ávido e que busca o prazer através do consumo dos bens e serviços diversificados, do outro, temos indivíduos dependentes, que os tornam fantoches do mercado. “Somos testemunhas de um conjunto de comportamentos desestruturados, de consumo patológico e compulsivo (LIPOVETSKY, 2007, p. 127).”

Refletindo: queremos uma vida simples e racional, sem luxo, sem o consumo frívolo? As lojas utilizam os termos à vista e a prazo como marketing para atrair o cliente. O cálculo que utilizamos para descobrir a vantagem do pagamento à vista ou a prazo pertence à Matemática Financeira. Quando uma loja sugere pagamentos a prazo, ela visa vantagem. Na maioria das vezes, esse tipo de pagamento não é vantajoso. Para a loja são mais rentáveis vendas a prazo, pois quando um cliente faz um pagamento parcelado, a empresa ganha em cima de juros pagos pelo cliente no financiamento da mercadoria. O vídeo sugerido a seguir faz parte da série “Eu e meu dinheiro” de uma iniciativa do Banco Central do Brasil. O vídeo apresenta dois jovens: um com atitudes racionais quando no ato de comprar e o outro reagindo com emoção, ao se deparar com possibilidades de comprar algo que não estava precisando. Os resultados das compras dos dois jovens são mostrados, de modo a evidenciar o descontrole financeiro de algumas pessoas quando, no ato de comprar, são imbuídas pela emoção e menos pelo racional. Vídeo: Eu vou levar - Série "Eu e meu dinheiro". Disponível em: . Compreendendo alguns aspectos financeiros: Empréstimo: é um contrato entre um cliente e uma instituição (banco, cooperativa de crédito, caixa econômica), pelo qual o cliente recebe uma quantia em dinheiro que deverá ser devolvida em prazo determinado, acrescida dos juros acertados. O dinheiro obtido não tem destinação específica. O cliente faz o uso que quiser Crédito pré-aprovado (cheque especial e cartão de crédito): é aquele que disponibiliza um limite de uso para o cliente, sem necessidade de burocracia. São instrumentos que permitem que se paguem compras e serviços sem necessidade de usar dinheiro no instante imediato da compra ou da contratação de um serviço. Financiamento: É um contrato entre um cliente e uma instituição financeira, mas com destinação específica. Exemplo: Aquisição de um veículo ou imóvel que funciona como garantia para o crédito. Mas há também financiamentos para serviços como estudos, viagens, tratamento dentário etc. Os empréstimos e financiamentos podem ser quitados antecipadamente, com redução dos juros, cabendo às instituições informar as condições para essa antecipação.

 

JUROS é a quantia gerada pela aplicação de um valor por determinado tempo a um percentual fixo. Essa aplicação pode ser constante (Juros Simples) ou capitalização acumulada (Juros Compostos)

JUROS SIMPLES (Crescimento linear): Acréscimos somados ao capital inicial no final da aplicação. É preciso distinguir os benefícios e os prejuízos de comprar a crédito. Conscientizando-se da diferença de custos dos produtos e serviços na situação de pagamento à vista ou a prazo. É necessário, ainda, Identificar os juros embutidos nas prestações de compras a crédito; saber optar pela melhor forma de pagamento para não ser penalizado.

Fórmulas:

 

Onde:

J representa os juros

C representa o capita/principal

i representa a taxa de juros

n representa o número de período

M representa o montante

Exemplo: Suponha que você vai fazer um empréstimo no valor de R$ 1.500,00 com uma pessoa da família. O acordo será para você quitar a dívida em seis meses e uma taxa de juros simples de 4%. Nessas condições, qual será o juro total da transação e qual será o montante ao final do período?

Ø  Cálculo de juros dos seis meses

J = 1.500 x 0,04 x 6

J = R$ 360,00

Ø  Cálculo do montante

M = 1.500 + 360

M = R$ 1.860,00

JUROS COMPOSTOS (Crescimento Exponencial): Acréscimos somados ao capital, ao fim de cada período de aplicação, formando com esta soma um novo capital, também conhecido como “juros sobre juros”. A partir desses cálculos é possível verificar se uma transação, como um empréstimo, por exemplo, é realmente viável. E também, analisar quando é melhor fazer o pagamento à vista, aplicar seu dinheiro em algum investimento, entre outras situações. Ao financiar algo utilizando juros simples, a pessoa obtém um montante (valor total a pagar) inferior ao que financia por meio de juros compostos.

Nota. Nessa modalidade de juros compostos, os cálculos dos juros acontecem de forma exponencial, ou seja, são cobrados juros sobre juros.

Fórmula

Onde:

M representa o montante

C representa o capita

i representa a taxa de juros

n representa o número de período

Exemplo:

Um comerciante fez um financiamento de R$ 50.000,00 para abrir um negócio. Ele vai pagar o valor do montante dividido em 24 meses e a uma taxa de 2,5% ao mês. Quanto ele pagará pelo empréstimo no final do período?

M = 50.000 (1 + 0,025)²⁴

M = 50.000 (1,025)²⁴

M = 50.000 (1,808725)

M = R$ 90.436,25

Observe que quanto maior o número de prestações, maior será o montante.

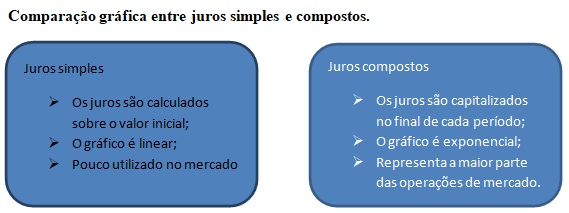
Representação gráfica dos juros simples e compostos

                                          

 

Referência bibliográfica

DANTAS, Venaide Maia. Planejamento financeiro na perspectiva de um consumo consciente: uma proposta de intervenção para o ensino da matemática financeira Mossoró, RN, 2019. Disponível em: <https://educapes.capes.gov.br/bitstream/

capes/561297/2/Produto%20Educacional%20 catalogado%20em%2021.01.2020.pdf>. Acesso em: 20 de jun. de 2020.

Caríssimos estudantes, o texto acima propõe as uma reflexão sobre um dos temas que impacta profundamente a vida financeira das pessoas. Ele trás conceitos relevantes sobre a educação financeira e a importância de saber poupar para ajustar as suas finanças pessoais e alcançar a sua liberdade financeira. Espero que vocês aproveitem bem a leitura, discuta com os seus familiares sobre o consumo consciente e possam incorporar tais conceitos na sua vida cotidiana. Bons estudos!

Atividade

1. Pesquise os preços de um produto na internet e veja qual é a melhor proposta para você, caso você fosse adquirir esse produto.

2. Pesquise e escreva no seu diário de bordo:

a) O significado da palavra inflação;

b) Como são calculados os indicadores INPC e IGP;

c) o que significa a palavra consumo;

d) o que quer dizer a palavra consumismo;

e) o que é marketing digital.

3. Aplicando hoje na caderneta de poupança a quantia de R$ 20.000,00, qual será o montante gerado ao final de 4 anos, sabendo que a rentabilidade mensal é de 0,5%? (Use a fórmula dos juros compostos).

Resposta: R$ 25409,78

4. Uma pessoa aplicou o capital de R$ 1.200,00 a uma taxa de 2% ao mês durante 14 meses. Determine os juros e o montante dessa aplicação.

Resposta: Juros R$ 336,00/ Montante R$ 1.536,00

5. Um investidor aplicou a quantia de R$ 500,00 em um fundo de investimento que opera no regime de juros simples. Após 6 meses o investidor verificou que o montante era de R$ 560,00. Qual a taxa de juros desse fundo de investimento?

Resposta: i = 2%.

BONS ESTUDOS!!!!

_____________________________________X__________________________________

     ROTEIRO DE ESTUDO

Componente Curricular: Matemática
Tema Norteador: USANDO A REALIDADE NA MATEMÁTICA

Laboratório: Laboratório de Aprendizagem de Matemática

Carga horária: 5H semanais
A atividade é referente: 08/06 à 22/06/2020

Caro estudante,

Este Roteiro tem como objetivo orientar os seus estudos individuais, durante esse período de atividades não presenciais. procure cumprir com responsabilidade e empenho as atividades propostas, anote suas dúvidas para tirá-las com o professor, nos momentos programados. Faça todas as anotações no seu caderno e diário de bordo.

https://enem.not.br/matematica-rio-no-jornal-nacional-a-matematica-do-cotidiano/

Por  Gláucio da Silva Freitas

Quando estamos pretendendo realizar uma atividade, dificilmente associamos a algum conhecimento matemático, ou até mesmo não fazemos a associação com nenhuma disciplina escolar. É importante observar que em todas as atividades que realizamos diariamente tem sempre um questionamento a se fazer relacionado a matemática.

Uma atividade que podemos pegar como exemplo é uma simples ida a padaria, você deve estar pensando, porque padaria? Digamos que pela manhã você vai a padaria comprar pão, em seguida você pensa em quantos pães comprar, ou seja, quantas unidades. Sabendo a quantidade que vai comprar vem o questionamento: qual o valor de dinheiro que vou gastar para fazer a compra? Evidentemente que temos primeiro que saber qual é o preço da unidade, cada unidade que nós formos comprando, temos de somar o valor. O valor total em dinheiro é a soma dos valores unitários, na prática se compramos 6 pães e o valor da unidade é igual a R$0,20, sabemos que o valor da compra é de R$1,20. Usamos valores numéricos para realizar esse raciocínio, abordando conceitos matemáticos importantes como o uso de unidades, soma e quantidade.

A matemática do dia a dia apresenta outras diversas formas de interpretação que não estão relacionados exclusivamente com a forma matemática concreta (matemática com o uso de números, teoremas).

Os atrasos e a correria do dia a dia são coisas que estamos sujeitos. Quantas vezes saímos de casa atrasados querendo em um certo intervalo de tempo chegar em algum lugar, ou desafiarmos até mesmo a capacidade de executar determinadas atividades. Nessa corrida contra o tempo utilizamos a matemática, realizamos cálculos mentais relacionados a quantidade necessária de tempo para concretizar determinadas atividades. Observe que a palavra quantidade aparece de novo em nosso estudo, enfatizando a atividade diária a matemática.

Nós mesmos conseguimos estabelecer a diferença entre o uso da matemática nas atividades, mas como podemos ver algumas coisas não realizaríamos sem a base de um ensino matemático, noções de soma, a questão de quantidade, os princípios básicos da contagem. Jamais ao realizarmos uma atividade relacionada ao calculo de tempo faríamos ligação a matemática, apenas sabemos que um intervalo de tempo pode significar muito ou pouco dependendo do conceito em que devemos relacionar o assunto.

Note que o estudo da matemática no dia a dia enfatiza o ensino da matemática como prática fora da escola, nos forçando por um lado a estudar suas aplicações dentro do local de ensino.

Bibliografia:

Etnomatemática - D'Ambrósio (1991).

Tudo é matemática - Ensino fundamental- Dante.

Matemática do ensino médio-Dante.

FREITAS, Gláucio da Silva. Usando a matemática no cotidiano. Disponível em

<https://www.infoescola.com/matematica/usando-a-matematica-no-cotidiano/>. Acesso em 06 de maio de 2020.

Caríssimos alunos, a proposta desse texto é fazer você refletir acerca do uso da matemática no cotidiano. Sugiro que você além de lê o texto também assista o vídeo sugerido na atividade para que você de fato possa compreender o porquê de estudar matemática na sua formação básica.

Espero que vocês aproveitem bem o conteúdo e possa usá-lo nas atividades práticas do dia a dia. 

Bons estudos!

Atividades

1. Assista ao vídeo abaixo e faça um comentário no blog sobre a importância da matemática na sua vida cotidiana. 

https://www.youtube.com/watch?v=6j1Rq2Zowlw

2. Os calçados surgiram como proteção para os pés e foram sofrendo alterações de acordo com a necessidade de quem os calçava.

                                                                  

A numeração dos sapatos foi criada em 1.324, na Inglaterra, no reinado de Eduardo II, tendo como unidade de medida um grão de cevada, que correspondia a 1/3 de polegada (lembrando que 1 polegada equivale a 2,54 centímetros). Hoje, os métodos ou sistemas de numeração de calçado baseiam-se em outras unidades de medida, mas não há uma uniformidade de padrões em termos internacionais.

No Brasil, o número de sapato está relacionado com o tamanho do pé, em centímetros, e é dado pela seguinte fórmula:

Onde N é o número do sapato e p é o tamanho do pé, em centímetros.

Com base nas informações, meça o tamanho do seu pé, aplique a fórmula e verifique se o resultado corresponde a numeração do seu sapato. Comente esse resultado no blog.

3. O que são e para que servem os códigos de barras?

Os números que você vê atrás dos produtos geralmente com um fundo branco e barras pretas são os códigos de barras, também chamados de códigos UPC e EAN (os mais comuns).

Todo produto possui um número de código de barras único, portanto, se você tem uma massa de macarrão com 500g e outra massa da mesma marca com 200g, ambos precisam de um número de código de barras. Assim, para cada sabor, cor ou variação diferente do produto que pretende vender, você precisa de um número de código de barras único.

Os códigos de barras foram criados para facilitar a integração entre produtos, mercadorias, caixas, etc. com o estoque. Antigamente havia um grande problema com filas enormes em caixas e falta de controle dos estoques dos produtos. O código de barras surgiu como solução para isso.

Código EAN-13

Esse é o código de barras mais comum utilizado para comercialização dos produtos de varejo no Brasil e, portanto, o mais utilizado por pequenas empresas e empreendedores.

Agora que você já sabe para que serve e como funciona o código de barras, procure na internet um código de barras e tente descobrir, através dos números a maior quantidade possível de informações sobre o produto.

https://pt.shopify.com/blog/69456645-guia-completo-sobre-codigo-de-barras-no-brasil

4. IMC é a sigla para Índice de Massa Corporal, que é um cálculo que serve para avaliar se a pessoa está dentro do seu peso ideal em relação à altura. Assim, de acordo com o valor do resultado de IMC, a pessoa pode saber se está dentro do peso ideal, acima ou abaixo do peso desejado.

Tabela de resultados do IMC

Cada resultado do IMC deve ser avaliado por um profissional de saúde. No entanto, a tabela a seguir indica os possíveis resultados do IMC, de acordo com a Organização Mundial da Saúde, sendo que o IMC entre 18,5 a 24,9 representa o peso ideal e o menor risco de algumas doenças.

Aplique a fórmula acima e veja em qual classificação você está. Aproveite e faça essa atividade com a sua família. 

___________________________________________x_____________________________________________

                                                                           ROTEIRO DE ESTUDO

Componente Curricular: Matemática
Tema Norteador: Desafios para Educação a Distância no Brasil

Laboratório: Laboratório de Aprendizagem de Matemática

Carga horária: 5H semanais
A atividade é referente: 25/05 à 08/06/2020

Caro estudante,

Este Roteiro tem como objetivo orientar os seus estudos individuais, durante esse período de atividades não presenciais. procure cumprir com responsabilidade e empenho as atividades propostas, anote suas dúvidas para tirá-las com o professor, nos momentos programados. Faça todas as anotações no seu caderno e diário de bordo.

Matemática: É possível aprender a distância?


                                  


Raquel Farina Barragan
Adaptado por: Jeam Clemente da Rocha

O aprendizado da matemática é de suma importância. Sua necessidade se evidencia na maioria das tarefas rotineiras, bem como é componente curricular de muitos cursos superiores, uma vez que é elemento imprescindível em diversas atividades profissionais. Por isso, o ensino e a aprendizagem da matemática vêm passando por diversas transformações e experimentos, tentando se adaptar as necessidades da sociedade em diversos contextos. Hoje, neste período de crise e com o isolamento social provocado pelo Covid-19 e pelo isolamento social, existe uma necessidade de todos os segmentos se reinventarem e buscar novas soluções para superarem esses novos desafios. O segmento da educação, fundamental para todos e para o crescimento do país, está vivenciando um momento de transformação sem ter se programado e nem planejado para enfrentar a crise.

Para minimizar o impacto negativo que essa paralização poderia trazer para a educação, surgiu como aporte o uso das tecnologias com maior intensidade, pois a mesma é facilmente acessível e leva a escola até o aluno, otimizando seu tempo e ampliando suas condições para acessar o conteúdo a qualquer momento. Mas como fazer com que o estudante aprenda as temáticas abordadas sem que as instituições de ensino tenham se preparado para esse enfrentamento? Como o docente (professor) e o discente (estudante) irão assumir o seu papel frente a esse novo desfio? Estes questionamentos estão mobilizando a comunidade acadêmica para buscar mecanismos que possam articular o ensino e a aprendizagem de forma mais efetiva. Um das preocupações ao se pensar no uso das tecnologias é como ensinar e aprender matemática. Assim, faz-se necessária a reflexão de como se dá o processo de ensino e aprendizagem da matemática nas condições oferecidas pelas tecnologias, uma vez que a disciplina exige prática e treino.

Experiências mostram que o ensino da matemática traz um protótipo de educação baseado em um padrão habitual de aprendizagem, onde a metodologia utilizada é narrativa, focada no discurso do professor, e os conteúdos são impostos como realidades incontestáveis, como algo finalizado e concluído, sem o cuidado em dar significado a esses conhecimentos. Os estudantes, por sua vez, têm apenas o trabalho de resolver uma série de exercícios que, muitas vezes, não exigem nenhum esforço criativo, reflexivo ou que exija capacidade de interpretação e raciocínio lógico. Esses estudantes não estão ligados sentimentalmente com essa disciplina e na maioria das vezes surgem questionamentos sobre a importância destas dentro do seu cotidiano. Isso advém, de modo geral, por conta de os conceitos serem trabalhados de forma aleatória, sem estarem inseridos em um contexto. Com isso perpetua-se o desenvolvimento nos estudantes das corriqueiras e constantes estratégias de simples memorização e repetição daquilo que foi estudado. Os estudantes, por sua vez, criam uma relação de dependência com o professor, sem buscar autonomia e sem adquirir qualquer senso crítico sobre aquilo que vem estudando. Desse modo começam a surgir às falhas no processo ensino/aprendizagem e que podem ser fruto da metodologia adotada pelo docente, da postura adotada pelo discente, de algum fator da Instituição ou da união das três.

Borba (2007) afirma que “quando o foco é aprendizagem matemática, interação é uma condição necessária no seu processo. Trocar ideias, compartilhar as soluções encontradas para um problema proposto, expor o raciocínio, são as ações que constituem o ‘fazer’ Matemático. E, para desenvolver esse processo a distância, os modelos que possibilitam o envolvimento de várias pessoas têm ganhado espaço, em detrimento daqueles que focalizam a individualidade”. Nesse contexto, fica evidente que o ambiente virtual está impregnado de relações sociais. 

Acredito que esse é um momento que devemos refletir acerca do cenário atual e nos esforçar para mudar essa realidade, para isso é preciso que cada um faça a sua parte, eu como docente e ao mesmo tempo aprendiz e vocês como discente e ao mesmo tempo professor. Para que as ações possam acontecer e gerar conhecimento é preciso o comprometimento de todos. Eu estou fazendo a minha parte, agora eu preciso que vocês façam a sua. 

Abaixo estão algumas sugestões de vídeos e após assistirem, resolvam

o que se pede em cada item e deixem os seus comentários no blog.

NÓS ACREDITAMOS NO POTENCIAL DE CADA UM DE VOCÊS PARA
MELHORAR A EDUCAÇÃO DO NOSSO PAÍS, SOBRETUDO A EDUCAÇÃO
DO NOSSO ESTADO.

Referência bibliográfica
SARAIVA, T. Educação a distância no Brasil: lições da história. Em aberto,
Brasília, ano 16, n. 70, abril/junho, 1996.
SBM, Projeto para educação a distância. Materiais didáticos de matemática
para EAD. Disponível em: www.sbm.org.br/EADSBM.doc Acesso em 25 de
agosto de 2015.
FARINA R. B. Matemática: é possível aprender a distância? São Paulo, 20
de outubro de 2015. Disponível em:
<http://www.ufjf.br/ebrapem2015/files/2015/10/gd6_raquel_barragan.pdf>.
Acesso em: 22 de maio de 2020.


Caríssimos estudantes, durante os próximos quinze dias iremos estudar
um dos mais importantes conteúdos da matemática, a “modelagem
matemática.” Nesse primeiro momento iremos utilizar os conceitos e aplicações
de função do primeiro grau. Para isso, fiz uma seleção de vídeos que abordam
essa temática e estou disponibilizando os links de acesso para vocês. A ideia
é realizar experimentos para analisar a aprendizagem de vocês através dessa
ferramenta e avaliar a sua eficácia na aprendizagem da matemática através
dessa tecnologia.

Vídeos sugeridos:
https://www.youtube.com/watch?v=R8UZRBFWJXY
https://www.youtube.com/watch?v=ExanYuFLLpg


Atividades I


1. Você teve dificuldade para entender a temática abordada no vídeo?


2. Após assistir os vídeos sugeridos você buscou outras fontes disponíveis na
rede que abordam esse mesmo tema?


3. Você acha que essa temática abordada é útil para sua vida?


4. Cite vantagens e desvantagens de estudar através de vídeo aula.


5. Se essa foi a primeira vez que você estudou uma temática usando essa
ferramenta, coloque o seu comentário no aqui e também no Blog.
Atividades II

Agora que você já assistiu aos vídeos, é hora de colocar em prática os seus
conhecimentos sobre a temática abordada.



1. Um vendedor que trabalha em uma loja de móveis localizada no bairro do
Vergel do Lago recebe mensalmente um salário composto de duas partes: uma
parte fixa, no valor de R$ 1.500,00, e uma variável, que corresponde a uma
comissão de 8% do total de vendas que ele faz durante o mês. Ele está
querendo elaborar a lei de formação matemática que determina o seu salário
mensal e qual será o seu salário estimado no final do mês se ele vendeu até o
dia 28 o valor de R$ 12.300,00. Ajude esse vendedor a resolver essa situação.


2. Um taxímetro marca uma quantia de R$ 3,50 mais R$ 1,1 por quilômetro
rodado. Suponha que você precise de um táxi para ir da praça padre Cícero até
o centro de Maceió

a) qual a lei de formação que determina o preço a ser pago?

b) se essa corrida tiver um percurso de km, qual o valor a ser pago por você?


3. O que determina o grau de uma função?


4. Abaixo está o desenvolvimento de um algoritmo (conjunto das regras e
procedimentos lógicos perfeitamente definidos que levam à solução de um
problema em um número finito de etapas) para encontrar o zero da função. Em
algum momento do desenvolvimento aparece um erro matemático. Identifique
esse erro.
𝒚 = −𝟐(𝒙 − 𝟏) − 𝟐 (I etapa)
𝒚 = 𝟎 (II etapa)
𝟎 = −𝟐(𝒙 − 𝟏) − 𝟐 (III etapa)
𝟎 = −𝟐𝒙 + 𝟏 − 𝟐 (IV etapa)
𝟐𝒙 = 𝟏 (V etapa)
𝒙 =𝟏/2  (VI etapa)


5. O que quer dizer zero a função do 1º grau?

VOCÊ NÃO PRECISA SER BOM EM TUDO, MAS NO QUE É, SEJA
EXCELENTE, EXTRAORDINÁRIO E EXPERT. Moisés Ribeiro

Bons estudos!

_______________________X_________________________


ROTEIRO DE ESTUDO

Componente Curricular: Matemática

Tema Norteador: O uso da Lógica para o Ensino de Matemática

Laboratório: Laboratório de Aprendizagem de Matemática

Carga horária: 5H semanais

Referente: 11/05 à 25/05/2020

Caro estudante,

Este Roteiro tem como objetivo orientar os seus estudos individuais, durante esse período de atividades não presenciais. procure cumprir com responsabilidade e empenho as atividades propostas, anote suas dúvidas para tirá-las com o professor, nos momentos programados. Faça todas as anotações no seu caderno e diário de bordo.

O que é lógica?

A lógica é uma área da filosofia que visa estudar a estrutura formal dos enunciados (proposições) e suas regras. Em suma, a lógica serve para se pensar corretamente, sendo assim, uma ferramenta do correto pensar.

Lógica tem origem na palavra grega logos, que significa razão, argumentação ou fala. A ideia de falar e argumentar pressupõe que o que está sendo dito possua um sentido para aquele que ouve.

Esse sentido fundamenta-se na estrutura lógica, quando algo "tem lógica" quer dizer que faz sentido, é uma argumentação racional.

A Lógica na Filosofia

Foi o filósofo grego Aristóteles (384 a.C.-322 a.C.) que criou o estudo da lógica, ele a chamava de analítica.

Para ele, qualquer conhecimento que pretenda ser um conhecimento verdadeiro e universal deveria respeitar alguns princípios, os princípios lógicos.

A lógica (ou analítica) passou a ser compreendida como um instrumento do correto pensar e a definição de elementos lógicos que fundamentam o conhecimento verdadeiro.

Os Princípios Lógicos

Aristóteles desenvolveu três princípios básicos que orientam a lógica clássica.

1. Princípio de identidade

Um ser é sempre idêntico a si mesmo: A é A. Se substituirmos A por Maria, por exemplo, fica: Maria é Maria.

2. Princípio da não-contradição

É impossível ser e não ser ao mesmo tempo, ou um mesmo ente ser também o seu oposto. É impossível que A seja A e não-A, ao mesmo tempo. Ou, seguindo o exemplo anterior: é impossível que Maria seja Maria e não seja Maria.

3. Princípio do terceiro excluído, ou terceiro excluso

Nas proposições (sujeito e predicado), só existem duas opções, ou é afirmativa ou negativa: A é x ou A é não-x. Maria é professora ou Maria não é professora. Não existe uma terceira possibilidade.

A Proposição

Em uma argumentação, aquilo que é dito e possui a forma de sujeito, verbo e predicado é chamado de proposição. As proposições são enunciados, afirmações ou negações, e possuem sua validade, ou falsidade, analisada logicamente.

A partir da análise de proposições, o estudo da lógica torna-se uma ferramenta para o correto pensar. O pensar corretamente necessita de princípios (lógicos) que garantam sua validade e verdade.

Tudo o que é dito em uma argumentação é a conclusão de um processo mental (pensamento) que avalia e julga algumas relações possíveis existentes.

O Silogismo

A partir desses princípios temos um raciocínio lógico dedutivo, ou seja, a partir de duas certezas prévias (premissas) chega-se a uma conclusão nova, que não está diretamente referida nas premissas. Isso é chamado de silogismo.

Exemplo:

Todo homem é mortal. (premissa 1)
Sócrates é homem. (premissa 2)
Logo, Sócrates é mortal. (conclusão)

Essa é a estrutura básica do silogismo e o fundamento da lógica.

Os três termos do silogismo podem ser classificados quanto à sua quantidade (universal, particular ou singular) e sua qualidade (afirmativa ou negativa)

As proposições podem variar quanto à sua qualidade em:

·       Afirmativas: S é P. Todo ser humano é mortal, Maria é trabalhadora.

·       Negativas: S não é P. Sócrates não é egípcio.

Também podem variar quanto à sua quantidade em:

·       Universais: Todo S é P. Todos os homens são mortais.

·       Particulares: Algum S é P. Alguns homens são gregos.

·       Singulares: Este S é P. Sócrates é grego.

Esta é à base da lógica aristotélica e de suas derivações.

Lógica Formal

Na lógica formal, também chamada de lógica simbólica, há a redução das proposições a conceitos bem definidos. Desse modo, o que é dito não é o mais importante, e sim, sua forma.

A forma lógica dos enunciados é trabalhada através da representação (simbólica) das proposições por letras: p, q e r. Também vai investigar as relações entre proposições através de seus operadores lógicos: conjunções, disjunções e condicionantes.

Lógica proposicional

Desse modo, as proposições podem ser trabalhadas de diversas formas e servir de base para a validação formal de um enunciado.

Os operadores lógicos estabelecem as relações entre proposições e tornam possível o encadeamento lógico de suas estruturas.

Negação

É o contrário de um termo ou proposição, representada pelo símbolo ~ ou ¬ (negação de p é ~ p ou ¬ p). Na tabela, para p verdadeiro, temos ~ p falso. (faz sol = p, não faz sol = ~ p ou ¬ p).

Conjunção

É a união entre proposições, o símbolo ∧ representa a palavra "e" (hoje, faz sol e vou à praia, p ∧ q). Para que a conjunção seja verdadeira, é necessário que ambas sejam verdadeiras. (Palavra-chave: intersecção ∩)

Disjunção

É a separação entre proposições, o símbolo v representa "ou" (vou à praia ou fico em casa , p v q). Para a validade, pelo menos uma (ou outra) deve ser verdadeira.

(Palavra-chave: intersecção ∪)

Condicional

É o estabelecimento de uma relação de causalidade ou condicionalidade, o símbolo ⇒ representa "se... então..." (se chover, então ficarei em casa, p ⇒ q).

Bi-condicional

É o estabelecimento de uma relação de condicionalidade nos dois sentidos, há uma dupla implicação, o símbolo ⇔ representa "se, e somente se,". (vou para a aula se, e somente se, não estiver de férias, p ⇔ q).

Lógica Computacional

A lógica computacional é derivada da lógica matemática, mas vai para além dessa, e aplicada à programação de computadores. Sem ela, diversos avanços tecnológicos, como a inteligência artificial, seriam impossíveis.

Esse tipo de lógica analisa as relações entre os valores e transforma em algoritmos. Para isso recorre também a modelos lógicos que rompem com o modelo inicialmente proposto por Aristóteles.

Esses algoritmos são responsáveis por uma série de possibilidades, desde a codificação e decodificação de mensagens até tarefas como reconhecimento facial ou a possibilidade de carros autônomos.

Enfim, toda a relação que se tem com os computadores, hoje em dia, passa por esse tipo de lógica. Ela mescla as bases da lógica tradicional aristotélica com elementos das lógicas chamadas de não-clássicas.

3. Lógicas Não-clássicas

Por lógicas não-clássicas, ou anticlássicas, reconhece-se uma série de procedimentos lógicos que abandonam um ou mais princípios desenvolvidos pela lógica tradicional (clássica).

Por exemplo, a lógica difusa (fuzzy), largamente utilizada para o desenvolvimento de inteligência artificial, não utiliza o princípio do terceiro excluso. Nela, admite-se qualquer valor real entre 0 (falso) e 1 (verdadeiro).

São exemplos de lógicas não-clássicas:

·       Lógica fuzzy;

·       Lógica intuicionista;

·       Lógica paraconsciente;

·       Lógica modal.

Lógica Matemática

A lógica matemática é derivada da lógica formal aristotélica e desenvolve-se a partir das suas relações de valores das proposições.

No século XIX, os matemáticos George Boole (1825-1864) e Augustus De Morgan (1806-1871) foram os responsáveis pela adaptação dos princípios aristotélicos para a matemática, dando origem a uma nova ciência.

Nela, as possibilidades de verdade e falsidade são avaliadas através de sua forma lógica. As sentenças são transformadas em elementos matemáticos e analisadas a partir de suas relações entre valores lógicos.

Um dos ramos da lógica concentra seus estudos na teoria dos conjuntos que na  educação básica tem a sua principal atenção na primeira série do Ensino Médio. Dessa forma, proponho a resolução das atividades propostas para lembrar as temáticas já estudadas no estudo de conjuntos e estabelecer a sua relação com a lógica matemática.

1. O complementar de A em relação a B:

(A) {2,5,7,11}

(B) {9}

(C) {0,2,4,5,7,11}

(D) {0,2,4,5,7,9,11}

(E) {5,7,11}

2. Da operação (A−B)∩(B−A):

(A) {2}

(B) ∅

(C) {1,4}

(D) {1,4,0}

(E) Nenhuma das anteriores

3. Da operação (A – B) ∪ (B – A), concluímos que:

(A) {2}

(B) Ø

(C) {1, 4}

(D) {1, 4, 0}

(E) Nenhuma das anteriores

4. Da operação A – B.

(A) {0, 2, 4, 6}

(B) {1, 4, 0, 9}

(C) {1, 4}

(D) {1, 4, 0}

(E) Todas as anteriores

5. Dados os conjuntos A = {0, 2, 4, 6, 8, 10} e B = {1, 3, 5, 7, 9, 11}, use o símbolo lógico ou para determinar a união dos conjuntos A e B.

6. Considere os conjuntos A = {1, 2, 3, 4, 5, 6}, B = {0, 2, 4, 6, 8, 10} e C = {0, -1, -2, -3}.

Use o símbolo lógico e para determinar as operações abaixo.

a) A e B

b) A e C

c) B e C

7. Considere os conjuntos A = {0, 1, 2, 3, 4, 5, 6, 7}, B = {0, 1, 2, 3, 4, 6, 7} e C = { }. Determine as seguintes diferenças.

a) A – B

b) A – C

c) C – A    

8. Dados os conjuntos A e B, dizemos que o complementar é formado por todo elemento que não pertence ao conjunto A em relação ao conjunto B, em que ele está contido, ou seja, . Com base na definição, considere os conjuntos A = {0, 1, 2, 3, 4, 5} e B ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} e determine o complementar de A em relação a B.

9. Suponhamos que A U B = {a, b, c, d, e, f, g, h}, A ∩ B = {d, e} e A – B = {a, b, c}, então:

a) B = {f, g, h}

b) B = {d, e, f, g, h}

c) B = { }

d) B = {d, e}

e) B = {a, b, c, d, e}

10. Num colégio de 100 alunos, 80 gostam de sorvete de chocolate, 70 gostam de sorvete de creme e 60 gostam dos dois sabores. Quantos não gostam de nenhum dos dois sabores?

FIM


ROTEIRO DE ESTUDO

Componente Curricular: Matemática

Tema Norteador: O uso da estatística na COVID-19

Laboratório: Laboratório de Aprendizagem de Matemática

Carga horária: 5H semanais



Caro estudante,

Este Roteiro tem como objetivo orientar os seus estudos individuais, durante esse período de atividades não presenciais. procure cumprir com responsabilidade e empenho as atividades propostas, anote suas dúvidas para tirá-las com o professor, nos momentos programados. Faça todas as anotações no seu caderno e diário de bordo.

1. Leitura e interpretação do texto sugerido dentro do tema gerador.

TEXTO

https://noticias.uol.com.br/colunas/marcos-silveira/2020/04/06/covid-19-o-grafico-da-curva-esta-nos-enganando.htm

2. Caro estudante, após a leitura desse texto você deverá responder dois blocos de exercícios. Na primeira semana você deverá responder o primeiro bloco referente à compreensão geral do texto que envolverá os seguintes componentes curriculares: matemática, L. Portuguesa e Biologia. Na segunda semana você deverá resolver o segundo bloco sobre os conhecimentos matemático/estatístico presentes no texto.

BLOCO 1 (PRIMEIRA SEMANA)

1. Qual a ideia principal do texto?

2. Na frase “Dessa forma, há uma sensação de que a curva da COVID-19 seja o GPS da quarentena” o que o autor quis dizer com isso?

3. Segundo a lei de Goodhart "Quando uma medida passa a ser o centro das atenções das decisões políticas, ele perderá seu valor como indicador." Para você, o que essa lei quer dizer?

4. O que o autor quis dizer com a frase “Achamos que entramos em um táxi e deixamos o motorista seguir o GPS?”

5. Existe uma preocupação do autor com relação a falta de precisão dos dados informados pelos órgãos oficiais de saúde. Segundo o mesmo, a doença ainda é pouco conhecida. Pesquise e elenque quais são os principais sintomas da Covid19.

3. Cada turma da primeira série do Ensino Médio deverá criar um grupo com os estudantes de cada classe para comparar e discutir as respostas da atividade principal. Após chegar a um consenso sobre essa atividade, cada grupo deverá eleger um coordenador que irá postar no blog da escola as respostas consolidadas de cada turma.

Quem luta está sujeito à morte, quem não luta já está morto. Deborah Karvalho

4. Observe os Gráficos:

FONTE:https://noticias.uol.com.br/colunas/marcos-silveira/2020/04/06/covid-19-o-grafico-da-curva-esta-nos-enganando.htm

Veja o gráfico oficial do Ministério da Saúde:

FONTE:https://noticias.uol.com.br/colunas/marcos-silveira/2020/04/06/covid-19-o-grafico-da-curva-esta-nos-enganando.htm

responda:

a. No último dia 3 de abril, o Ministério da Saúde divulgou o Boletim Epidemiológico 6 - sobre o Coronavírus. Nele está a real dimensão do problema: a análise das hospitalizações por Síndrome Respiratória Aguda Grave (SRAG) no Brasil em 2019 e 2020. Para fazer esta análise estatística, foi utilizado um Gráfico de dupla entrada. Faça uma pesquisa e escreva com suas próprias palavras o que é um gráfico de dupla entrada e porque ele foi utilizado para fazer essa representação.

b. Construa uma tabela que represente os dados do primeiro gráfico em uma tabela de distribuição e descubra onde ocorreu o pico de hospitalizações no ano de 2019.

c. O segundo gráfico mostra uma curva que no primeiro momento se assemelha a uma curva exponencial. É comum escutar o termo EXPONENCIAL. Você sabe o que quer dizer esse termo? Faça uma pesquisa e escreva a definição de função exponencial e relate qual a sua relação com o crescimento do covid19.

d. Com relação ao primeiro gráfico, em qual período (semana) ocorreu o pico das hospitalizações por Síndrome Respiratória Aguda Grave (SRAG)?

e. No primeiro gráfico, qual o aumento percentual de casos de SRAG entre a primeira e a oitava semana?

f. Com os grupos das turmas da 1ª série já criados, comparem e discutam as respostas da atividade principal para chegarem a um consenso sobre as estas atividades propostas durante a segunda semana, em seguida poste no blog da escola as respostas consolidadas de cada turma.

BONS ESTUDOS!